How to Draw the Oval of the Oval Office

How to Draw the Oval of the Oval Office

Michael S. Schneider, B.S., MEd. Mathematics

The Oval Office in the White House is arguably the most important room in the world.

The official White House Museum article about the Oval Office describes it as:

"The Office of the President -- The Oval Office is the president's formal workspace, where he confers with heads of state, diplomats, his staff, and other dignitaries;
where he often addresses the American public and the world on television or radio; and where he deals with the issues of the day."

The history of the White House is fascinating, as is the history of the Oval Office itself.

This elegant space at the West Wing's southeast corner was designed in 1933-34 by architect Eric Gugler (1889-1974).

The geometry of its wooden floor (without the carpeting, seen below) presents us with an optical illusion.
There appear to be three-dimensional steps leading to the door. This shows us that great thought went into the room's design.

I was wondering whether the Oval office was designed mathematically, and whether it's the kind of oval known as an ellipse.
People often confuse an oval with an ellipse.

If it's also an ellipse it would be easy to construct geometrically.

An ellipse always has two axes of reflection, a major axis and a minor axis; an oval has one or more axes.
So an ellipse is always an oval, but an oval may or may not be an ellipse.
An egg-shape is an oval but not an ellipse. (The word "oval" derives from ovum the Latin for "egg".)

Is the Oval Office also an ellipse?

From its dimensions and the photographs I've seen, the Oval Office does seem to be a kind of oval that's also an ellipse.

I haven't been able to find an architectural drawing that accurately depicts the oval of the Oval Office with its published dimensions:

Long axis: 35' 10" (10.9m)
Short axis: 29' (8.8m)
(Room Height: 18' 6" (5.6m))

so I've drawn it:

35' 10" = 430 inches
29' = 348 inches

And 430/348 = 1.2356...

Does this ratio remind us of anything?
Such important space requires special geometry, and immediately the elegant Golden Ratio comes to mind.

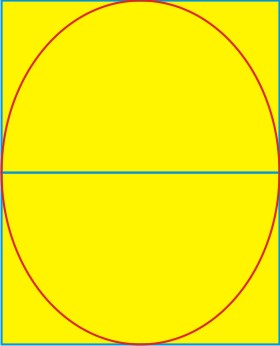
In fact, two Golden Rectangles stacked along their long side have virtually this same ratio:

2/Phi = 2/ (1+sqrt5)/2 = 4/ (1+ sqrt5) = 1.2360...

The difference between 1.2356... and 1.2360... is very slight. If the room was less than 3/16ths of an inch longer the match would be precise (348 x 2/Phi = 430.1516... inches).

Thus, within excellent tolerance, it feels safe to say that the oval of the Oval Office is one designed within two Golden Rectangles!

These are the same two Golden Rectangles we carry around in the proportions of our forearms (and throughout our entire body),
seen when we hold our arms out and bend our wrists (if we can) at right angles.

If we had used the dimensions provided in metric measure, the Golden Ratio connection would be less recognizable: 10.9m/8.8m = 1.2386...
That's why it's important, if possible, when studying the dimensions of art and architecture, to use the same metrological system as the original designers.

There appears to have been greater use of the Golden Ratio in the design of the White House as a whole, so an Oval Office incorporating this ratio would place it in a consistent geometric context.

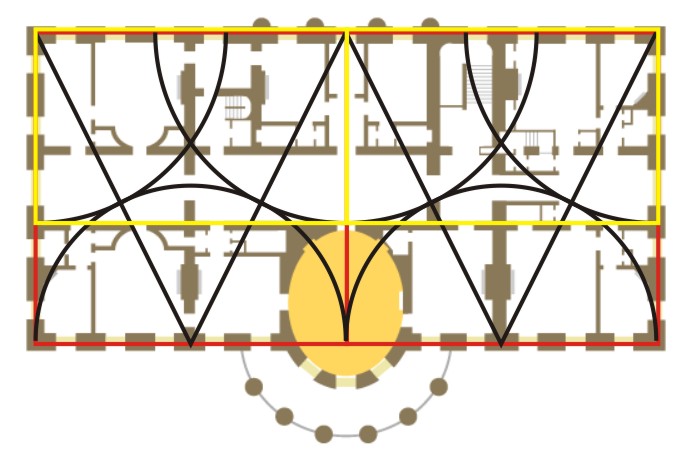
The White House as a whole appears to be intentionally designed in two squares, seen in this plan of the second floor, showing the lovely Yellow Oval Room (originally the Library) opening onto the Truman Balcony:

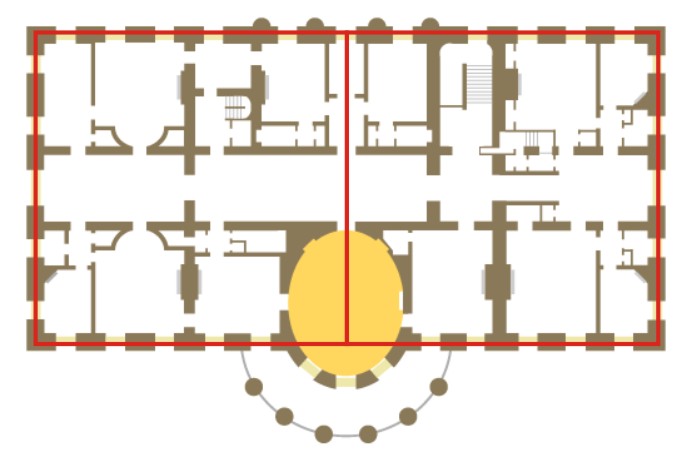
Dividing each square by the Golden Ratio shows that one wall along the central hall lies along the edge of a Golden Rectangle and smaller Phi-squared rectangle:

Doing this in the opposite direction defines the other wall along the hall:

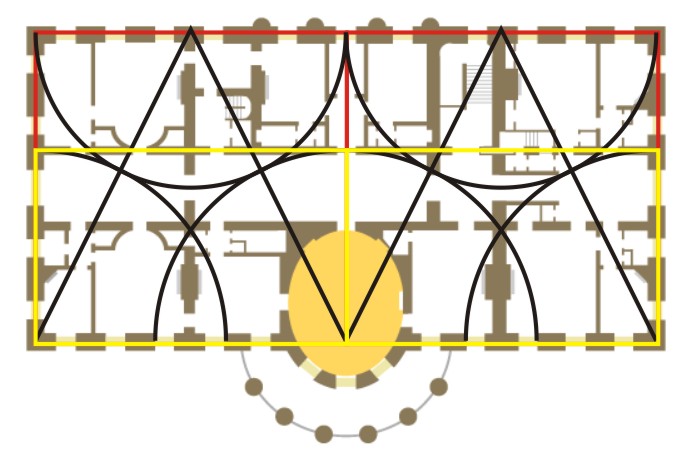
Thus the second floor of the White House seems to be designed as overlapping pairs of Golden Rectangles.
I leave it to the reader to apply further turns of a geometric compass
to show how the individual rooms and other spaces are made of combinations of smaller Golden Rectangles and squares and their simple divisions.

Constructing the Oval of the Oval Office

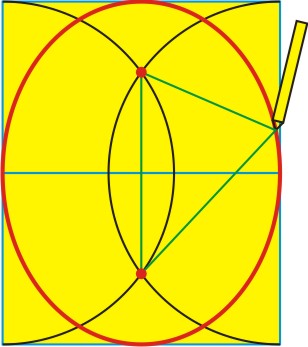
The method for drawing the oval/ellipse of the Oval Office as found in two Golden Rectangles, seen below, is the same as for any rectangle:

Place your compass at the midpoint of a long side and open it to the corner.
Turn a half-circle. Do the same on the other long side.

The two (red) points where they cross are the two foci of the future ellipse.

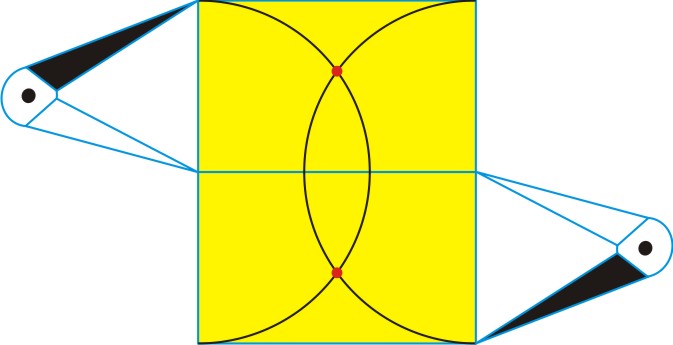
Press a push-pin tack into each of the focal points.

Then tie a piece of string into a loop that stretches from one focal point, past the other, and to the short side of the whole rectangle, seen here:

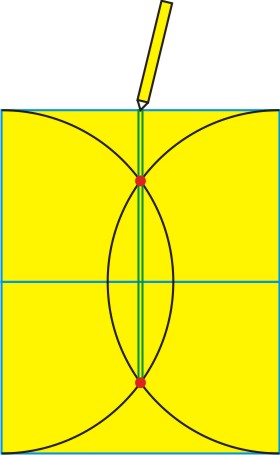
Place your pencil into the loop at its extreme end and keep a steady tension as you allow the loop to guide you around its unique elliptical path.

By doing this construction you're replicating the ellipse of the famous Oval Office.

Personally, I'm glad to know that the Golden Ratio, the most beautiful, inspiring, organic and uplifting of ratios,
guides the proportions of the room (and building) where many of the most important decisions in the world are made.

Constructing The Universe Home Page